Let $G$ be a graph. A $k$-strong-edge-coloring is a function $c : E(G) \to \{1,\dots,k\}$ where every color-class forms an induced matching. That is, two edges of the same color are not incident and do not have adjacent endpoints. Equivalently, a $k$-strong-edge-coloring is a $k$-coloring of the square of the line graph. The strong chromatic index, denoted $\chi_s(G)$, is the minimum $k$ such that a $k$-strong-edge-coloring exists for $G$.

Many people have studied the strong chromatic index of planar graphs which are subcubic (maximum degree at most three).

Theorem. (Kostochka et al. 2015+). If a graph $G$ is planar and subcubic then $\chi_s(G) \leq 9$.

Other sparsity conditions can imply stronger bounds on the strong chromatic index. For instance, if we force the girth of a planar graph to be high, then it becomes easier to color.

Theorem. (Hocquard et al. [8]). Let $G$ be a subcubic planar graph with girth $g$.

1. If $g \geq 14$, then $\chi_s(G) \leq 6$.
2. If $g \geq 10$, then $\chi_s(G) \leq 7$.
3. If $g \geq 8$, then $\chi_s(G) \leq 8$.

The potentially optimal number of colors for a graph with maximum degree $\Delta$ is $2\Delta-1$. In this scenario, there is a sequence of results.

Theorem. Let $G$ be a graph with $\Delta(G) \leq d$.

1. (Borodin and Ivanova) If $d = 3$, $G$ is planar, and $G$ has girth at least $41$, then $\chi_s'(G) \leq 5$.
2. (Borodin and Ivanova; implicit) If $d = 3$, $G$ has girth at least $9$, and $\operatorname{mad}(G) < 2 + \frac{2}{23}$, then $\chi_s'(G) \leq 5$.
3. (Borodin and Ivanova) If $d > 3$, $G$ is planar, and $G$ has girth at least $40\lfloor \frac{d}{2}\rfloor +1$, then $\chi_s'(G) \leq 2d-1$.
4. (Borodin and Ivanova; implicit) If $d > 3$, $G$ has girth at least $8\lfloor \frac{d}{2}\rfloor + 1$, and $\operatorname{mad}(G) < 2 + \frac{2}{24\lfloor \frac{d}{2}\rfloor - 1}$, then $\chi_s'(G) \leq 2d-1$.
5. (Chang, Montassier, Pêcher, Raspaud) If $d > 3$, $G$ is planar, and $G$ has girth at least $10d+46$, then $\chi_s'(G) \leq 2d-1$.
7. (Chang, Montassier, Pêcher, Raspaud; implicit) If $d > 3$, $G$ has girth at least $2d+10$, and $\operatorname{mad}(G) < 2 + \frac{2}{6d+26}$, then $\chi_s'(G) \leq 2d-1$.
8. (Wang and Zhao) If $d > 3$, $G$ is planar, and $G$ has girth at least $10d-4$, then $\chi_s'(G) \leq 2d-1$.
9. (Wang and Zhao) If $d > 3$, $G$ has girth at least $2d-1$, and $\operatorname{mad}(G) < 2 + \frac{1}{3d-2}$, then $\chi_s'(G) \leq 2d-1$.
10. (DeOrsey, Diemunsch, Ferrara, Graber, Harke, Jahanebkam, Lidický, Nelsen, Stolee, Sullivan)
    If $d = 3$, $G$ is planar, and $G$ has girth at least $30$, then $\chi_s'(G) \leq 5$.
11. (DeOrsey, Diemunsch, Ferrara, Graber, Harke, Jahanebkam, Lidický, Nelsen, Stolee, Sullivan)
    If $d = 3$, $G$ has girth at least $9$, and $\operatorname{mad}(G) < 2 + \frac{1}{7}$, then $\chi_s'(G) \leq 5$.
12. (DeOrsey, Diemunsch, Ferrara, Graber, Harke, Jahanebkam, Lidický, Nelsen, Stolee, Sullivan)
    If $d = 4$, $G$ is planar, and $G$ has girth at least $28$, then $\chi_s'(G) \leq 7$.
13. (DeOrsey, Diemunsch, Ferrara, Graber, Harke, Jahanebkam, Lidický, Nelsen, Stolee, Sullivan)
    If $d = 4$, $G$ has girth at least $7$, and $\operatorname{mad}(G) < 2 + \frac{2}{13}$, then $\chi_s'(G) \leq 7$.

The theorems above are implied by a sparsity condition using the maximum average degree of a graph (and some forbidden subgraphs). A related result implies that the list-coloring version of strong chromatic index is bounded by five for subcubic planar graphs with girth at least 41. All results use discharging in some manner, either explicitly or implicitly.

There are three main software components.

• SCI_magma.txt is a list of Magma commands to discover the coefficient of a polynomial to use in a Combinatorial Nullstellensatz argument. (Written by Phil DeOrsey)
• SCI_Sage_code.sage is a list of Sage commands to discover the coefficient of a polynomial to use in a Combinatorial Nullstellensatz argument. (Written by Stephen G. Hartke)
• StrongEdgeColorings.sws is a Sage worksheet that contains many helpful routines, including constructing the configurations. It also tests the base cases of the main theorem regarding strong 5-edge-colorings.
• strong_edge_reducible.c is a C program that tests if a configuration is reducible.

  To compile, place this file in the nauty/ folder after unpacking the nauty source code, available at http://cs.anu.edu.au/~bdm/nauty/

  Compile using the following command:

  gcc -o strong_edge_reducible strong_edge_reducible.c nauty.o nausparse.o nautil.o gtools.o

  Then, run : strong_edge_reducible.exe < configurations.txt

  or (for 7 colors) : strong_edge_reducible.exe -k 7 < configurations.txt

• YColoring.sws is a Sage worksheet that determines that no $3$-vertex $v$ can have $N_3(v)$ consist entirely of vertices $u$ with $|\operatorname{Resp}(u)| \geq 12$. (Written by Bernard Lidický)

• configurations.txt is the input file for strong_edge_reducible.exe containing all configurations, reducible or not.
• ser_output.txt is the output file reporting which configurations are reducible or not.
• caterpillars-d4.txt is the input file for strong_edge_reducible.exe containing a list of $(t,4)$-caterpillars.
• caterpillars-d5.txt is the input file for strong_edge_reducible.exe containing a list of $(t,5)$-caterpillars.
• caterpillars-d6.txt is the input file for strong_edge_reducible.exe containing a list of $(t,6)$-caterpillars.
• reducible-d4y.txt is the input file for strong_edge_reducible.exe containing a list of $Y_4(t_1,t_2,t_3)$ configurations.
• reducible-d4y-out.txt is the output file for strong_edge_reducible.exe -k 7 < reducible-d4y.txt demonstrating which $Y_4(t_1,t_2,t_3)$ configurations are 7-reducible.

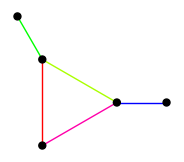
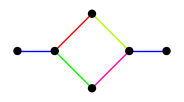
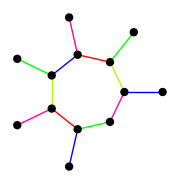
Here are some strong edge colorings that were used as base cases in the proof.

This collaboration began as part of the 2014 Rocky Mountain/Great Plains Graduate Research Workshop in Combinatorics, supported in part by NSF Grant #1427526. The collaboration continued at the the 2015 Rocky Mountain/Great Plains Graduate Research Workshop in Combinatorics, supported in part by NSF Grant #1500662. Michael Ferrara is supported in part by Simons Foundation Grant #206692. Stephen G. Hartke is supported in part by Simons Foundation Grant #316262.