Let $c : E(G) \to \{1,\dots,k\}$ be a coloring of the edges of a graph $G$. For a vertex $v \in V(G)$, let $\overline{c}(v) = (t_1,\dots,t_k)$ where $t_i$ is the number of edges incident to $v$ that have color $i$. Then, sort the values of $\overline{c}(v)$ to find the color-blind partition $c^*(v)$. We say that a coloring $c$ is color-blind distinguishing if $c^*$ is a proper vertex-coloring. The minimum $k$ such that a color-blind distinguishing $k$-coloring exists is the color-blind index of $G$.

Unlike normal vertex or edge colorings, there does not always exist a color-blind distinguishing coloring. All known examples of graphs with no such coloring have minimum degree at most three.

As part of GRWC 2014, we investigated these low-degree graphs. We gain a lot more information about graphs of low degree that have or do not have color-blind distinguishing colorings. We study several classes of graphs, including bipartite regular graphs, 3-regular graphs where every vertex is in at least one 3-cycle, and cacti.

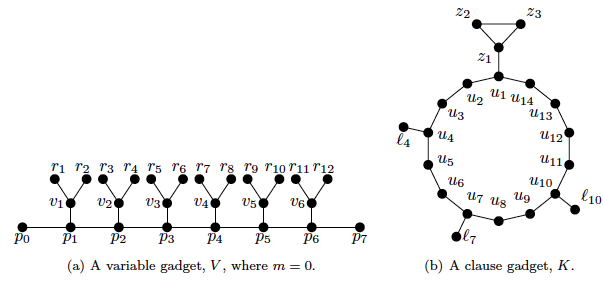
The investigation becomes more complicated as we find that it is NP-complete to distinguish between color-blind index 2 or 3.

ColorBlindIndex.sws is a Sage worksheet that contains many helpful routines, including constructing and testing the reducible configurations.

This collaboration began as part of the 2014 Rocky Mountain/Great Plains Graduate Research Workshop in Combinatorics, supported in part by NSF Grant #1427526.