The ADAGE Framework is a general-purpose framework for automating discharging arguments. Since an adage is a short phrase that conveys a deeper meaning, so does an adage proof provide a very short description of a discharging argument such that a computer can perform the long case analysis to verify the argument. This framework is planned to expand to several domains, but currently is only implemented for density problems on grids.
The framework has four distinct steps.
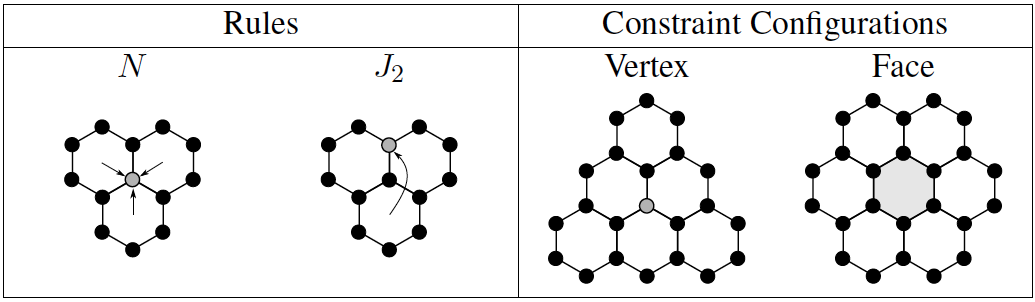
- Define notions of forbidden and/or reducible configurations.
- Define a charge function and design discharging rules. (But do not assign value!)
- Construct all possible arrangements of discharging rules simultaneously acting on an object, and create a linear constraint for each.
- Solve a linear program that assigns value to the discharging rules such that the discharging assertions are guaranteed.
This way of constructing a linear program using combinatorial generation and solving it to find "the best proof using these structures" is very similar to the use of semidefinite programming in Razborov's flag algebras.
If $G$ is a plane grid, then let $X \subset V(G)$ be a set of vertices satisfying some property. We aim to define a lower bound on the density of $X$, defined as
The ADAGE framework was implemented for density problems in grids, especially attacking identifying codes and variations on identifying codes. The main theorem is the following bound that improves on all previous human-written proofs.
Theorem. The minimum density of an identifying code in the hexagonal grid is at least $\frac{23}{55} = 0.4\overline{18}$.
This does not yet match the current-best upper bound of $\frac{3}{7} \approx 0.428571$. However, the framework was able to reproduce the following sharp results.
Theorem (Ben-Haim and Litsyn). The minimum density of an identifying code in the square grid is $\frac{7}{20}$.
Theorem (Karpovsky, Chakrabarty, and Levitin). The minimum density of an identifying code in the triangular grid is $\frac{1}{4}$.
Theorem (Honkala). The minimum density of a locating-dominating code in the hexagonal grid is $\frac{1}{3}$.
Theorem (Slater). The minimum density of a locating-dominating code in the square grid is $\frac{3}{10}$.
Theorem (Seo and Slater). The minimum density of an OLD code in the hexagonal grid is $\frac{1}{2}$.
Theorem (Seo and Slater). The minimum density of an OLD code in the square grid is $\frac{2}{5}$.
Theorem (Kincaid, Oldham, and Yu). The minimum density of an OLD code in the triangular grid is $\frac{4}{13}$.
Web Version ArXiv Version
The ADAGE Framework is available as open-source software. You can find the most-recent version at the GitHub page or at my software web page. You can also download the software here:
- adage-grids.zip contains the C++ code for ADAGE on Grids, along with the output data.
- TreeSearch is required in order to generate constraints.
- Utilities is required for some helpful macros and data structures.
- CPLEX is required for solving linear programs.
Slides
Slides