Given a group $\Gamma$ acting on a set $X$, a $k$-coloring $\phi:X\to\{1,\dots,k\}$ of $X$ is distinguishing with respect to $\Gamma$ if the only $\gamma\in \Gamma$ that fixes $\phi$ is the identity action. The distinguishing number of the action $\Gamma$, denoted $D_{\Gamma}(X)$, is then the smallest positive integer $k$ such that there is a distinguishing $k$-coloring of $X$ with respect to $\Gamma$. This notion has been studied in a number of settings, but by far the largest body of work has been concerned with finding the distinguishing number of the action of the automorphism group of a graph $G$ upon its vertex set, which is referred to as the distinguishing number of $G$.

The distinguishing number of a group action is a measure of how difficult it is to ``break'' all of the permutations arising from that action. In this paper, we aim to further differentiate the resilience of group actions with the same distinguishing number. In particular, we introduce a precoloring extension framework to address this issue. A set $S \subseteq X$ is a fixing set for $\Gamma$ if for every non-identity element $\gamma \in \Gamma$ there is an element $s \in S$ such that $\gamma(s) \neq s$. The distinguishing extension number $\operatorname{ext}_D(X,\Gamma;k)$ is the minimum number $m$ such that for all fixing sets $W \subseteq X$ with $|W| \geq m$, every $k$-coloring $c : X \setminus W \to [k]$ can be extended to a $k$-coloring that distinguishes $X$.

• $\operatorname{ext}_D(\mathbb{R},\operatorname{Aut}(\mathbb{R}),2) =4$ where $\operatorname{Aut}(\mathbb{R})$ is comprised of compositions of translations and reflections.
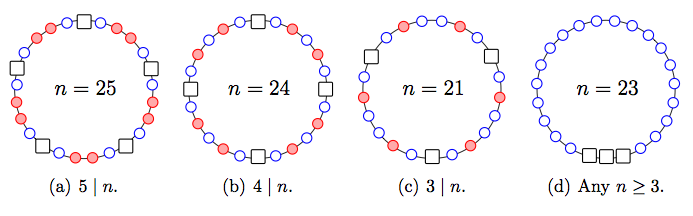
• $\operatorname{ext}_D(C_n) = 4$ if the smallest prime divisor of $n$ is at least 7.
• $\operatorname{ext}_D(C_n) \leq \operatorname{ext}_D(\mathbb{R}/\mathbb{Z}) \leq 16$.

Michael Ferrara was supported by Simons Foundation Grant #206692. Stephen Hartke was supported by NSF grant DMS-091485.

List Distinguishing Number

On the arXiv, Computational Combinatorics (Blog).